My all-time favorite piece of software is Graphing Equations and Green Globs. The program has several components but Green Globs is what stole my heart.

Figure 11-7
The game is simple to understand. When you start up the novice game, thirteen globs appear randomly scattered on a coordinate grid. (See figure 11-7.) The student’s goal is to explode all the globs by hitting them with graphs of equations entered in an input box. The scoring algorithm encourages students to hit as many globs as possible with each equation. For example, in figure 11-7 the equation Y = -2 will draw a line that will hit the two globs located at (7,-2) and (9,-2), because they share the same y-coordinate, -2. Since the point total doubles for each glob you strike with one equation, hitting two globs results in a score of 1 + 2 = 3 points.
A better choice would have been y = 1/3x + 4.5, because it would have hit three globs, and the scoring would have been 1 + 2 + 4 = 7 points. With some adjusting of the line (made possible by an undo button), you can hit four globs, for a score of 1 + 2 + 4 + 8 = 15 points. Can you see how? (y = 1/5x + 4) The globs are generous. You just have to touch them to score a hit.
Guillermo’s Big Score
Guillermo was a student who didn’t like math. He found his eighth-grade algebra book a big snore, mostly because he didn’t like to read difficult formal language, which is the style of most algebra textbooks. He also was a problem for his teacher, as he liked to interact with his fellow students when he should have been paying attention to the teacher. I was in the room one day when the teacher told him to sit in the back of the room by himself so he wasn’t such a distraction for other students, who also would have preferred to do something other than listening to the teacher drone on about the contents of the day’s lesson. On this occasion, I shared Green Globs with the class. I even got the attention of Guillermo, who found the game interesting. The teacher brought in a cart full of laptops, and Guillermo had a chance to play. He caught on very quickly and helped other students. Unfortunately, the game was not readily available to him, because the laptop cart was shared by all the eighth-grade students in the school. There was little chance that Guillermo would have the opportunity to play the Globs game again, as the teacher treated this activity more as a frill than as something to get serious about. But then, unbeknownst to me, serendipity stepped in and took Guillermo on an interesting ride. One of the reasons he was a discipline problem in his current class was that he believed he should have been in the gifted and talented (G/T) eighth-grade class. When he discovered that the G/T teacher was teaching Globs, he found a way to absorb what the G/T teacher was teaching. He learned about the expert game of Globs, which allowed the use of the sine function, which he knew could knock out all the globs with one shot. However, in the expert game, there were blockers (unfilled circles) that prevented an easy knockdown of all the globs.

Figure 11-8
In figure 11-8, y=10sin(10x) would knock down all the globs if it weren’t for the blockers.
Guillermo learned how to control the sine curve. He figured out that by adding a linear term like x + 1 to the 10sin10x term and shrinking the frequency (coefficient) of the sine term, he could squeeze the curve between the blockers on a diagonal and hit five globs for a score of thirty-one points.

Figure 11-9
By changing the coefficient of the sine term to 3, three more globs were blown up, for a total of 255 points.

Figure 11-10
By manipulating the coefficients through trial and error, the two other globs could be taken care of as well, to get the score to 1,023. This could take a long time, but I was sure Guillermo was willing to put in the time on his own. One late afternoon, I got a phone call from the teacher, telling me that Guillermo had come up with an amazing score. He had hit all thirteen globs with one shot! I went to see his accomplishment the next day. This was the array of globs that he solved.

Figure 11-11
Here’s the function (see figure 11-12) that he came up with and the graph it
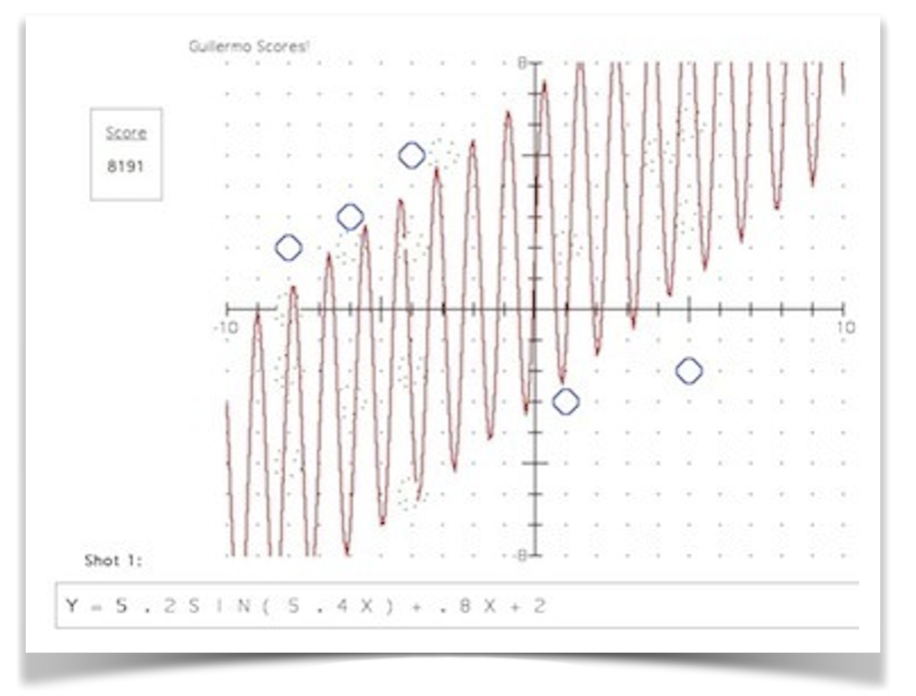
Figure 11-12
produced. Thirteen globs on one shot is worth 1+2+4+8+16+32+64+128+256+512+1024+2048+4096 = 8191 points. It’s also the same as 2^13 – 1 points, with the 13 matching the number of globs hit! Not bad for a failing math student.
Green Globs is available at http://greenglobs.net
Source of this post is chapter 11 – “Microworlds and Beyond” in my book The Wannado Curriculum: A Math Teacher’s Journey to the Dynamic Math 2.0 Classroom – Amazon
Note: Desmos has two activities Linear Slalom and Parabola Slalom that get after some of the same skills as Green Globs requires but its too structured and not as much fun. If you can’t use Globs give the Slaloms a try.
I have recently returned to the classroom after 13 years in the oilfield and cannot find green globs. Can anyone direct me to a place to acquire the software?
http://greenglobs.net