
| WhatŐs needed... Resources: Shoe box tops; toothpicks; computer applet and Geometer's Sketchpad Classroom Environment: Students in groups with access to computers; teacher demonstration station. Strategy: Groups work together to come up with a group prediction through experimentation. |
One of the reasons probability is one of my favorite topics to teach is that it can lead to many surprises along with some useful math done in interesting ways. The challenge in this activity is to see if students can make a prediction about the likelihood of toothpicks landing on lines when dropped randomly using experimental and theoretical data.
Preliminaries
- Make a set of shoebox top toothpick tossing ŇarenasÓ.

- Draw equidistant, parallel lines inside the shoebox top. The distance between the lines should be the same as the length of the toothpicks. Make one of these for each of your groups.
- If you don't have the
boxes, you can demonstrate the experiment by
dropping the toothpicks on a tiled floor. Here I
dropped a bunch on a hardwood floor. (See photo
below. I highlighted the toothpicks and lines on the
floor. An adjustment will need to be made since the
toothpicks will not be the same as the perpendicular
distance between lines.)

Setting the Stage
- Have your students sit in
groups or teams. You are facing them standing next
to your one computer station. (Maybe even projecting
on a digital white board.) Show them an arena for
the experiment.
- Tell your class that they
will be answering a question that was originally
posed by a man named Georges-Louis Leclerc, Comte de
Buffon about 250 years ago. "Suppose we have a floor
made of parallel strips of wood, each the same
width, and we drop a needle onto the floor. What is
the probability that the needle will lie across a
line between two strips?" (source: Wikipedia)
- Take guesses from your
class. Then ask them to explain their guess.
- Ask them: How might we
proceed to find out which student or group made the
best guess? LetŐs do the experiment to help us find
out.
- Hand out the activity sheet. Make sure the students understand the instructions.
- Each group will drop 50 toothpicks 10 at a time on their parallel lined arena.
- Students toss the toothpicks and make their predictions about what the class crossing average will be.
- By Group - Worksheet 1

- By Class - Worksheet 2
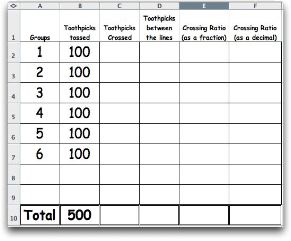
- Complete worksheet 2 with the class. Who had the best guess? (Compare the group results with individual group guesses.)
- After finishing, ask the
students how they might come up with even a better
or best "guess"? (Theoretical probability is 2/Pi or
approximately .6366197. See part
2 for more detail.)
- Go to this website: http://www.metablake.com/pi.swf
- Can you explain what is happening?
- How did Pi get into the act? Hint: Double your number of your individual throws and divide it by the number of crosses. What do you get? Check with other groups. What can you conclude? (Your answer is an approximation for Pi.)
- Why does this happen? (See
George Reese's explanation.)
- Estimating Pi. Video. Teacher TV. Buffon's experiment explained using french bread and taped lines!


- Another excellent
simulation. Calculating
Pi using Buffon's Needle. (Watch the video
first!)
