Part 2: Here I want to explain in a bit more detail George Reese's excellent description of the simplest case of the needle experiment.

Determining the probability that a dropped toothpick will cross on a line.

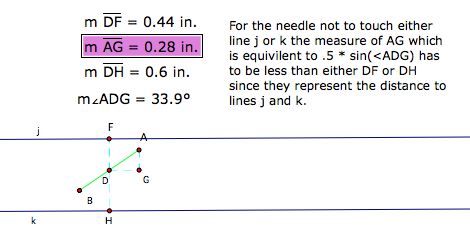
Click above to download Sketchpad sketch

The diagram above is a Sketchpad version of the figure that appears in George's explanation. In order to come up with a probability he considers the two relevant variables: (1) the perpendicular distances from the center of the needle to lines j and k and (2) the orientation of the needle in degrees. In the example above, we know the needle does not cross a line. We can measure the perpendicular distance from the midpoint of the needle (D) to each of the parallel lines j and k. Those distances are DF and DH. What makes the needle not cross a line is the fact that AG is half of the sine of angle ADG.

By definition the sine of angle ADG is the length of the opposite side (AG) divided by the hypotenuse (.5). Therefore, AG = .5 * sin <ADG.

Note that in the diagram above AG is shorter than both DF and DH. If AG is greater than either DF or DH there would be a crossing. Download and experiment with the sketch to confirm this.

If we graphed our data we could see that the hits occur in a special region of the rectangle.

The distance between the lines is 1 inch. The needle is one inch. So the midpoint that's closest to either j or k will be somewhere between 0 and.5 from the line. However if neither of the segments is greater than AG the point would plot above the curve and not counted as a hit.

The area under the curve is 1. The area above the curve is .5 * Pi - 1 or approximately 1.57. So the probability would be 1 / Pi/2 = 2 / Pi. So if the rectangle was a dart board, and every point on the board was a possible the probability would be 2/Pi or .6366197 almost 2/3 of the needles will cross a line.

Back to part 1.

  Updated: 3.19.13