Method 2:
Another way to find areas of polygons is to use Pick's
Rule. To find out what Pick's rule is do the discovery
activities below.
Lattice Grid Points and Area
Part 1: Below are some polygons with no points
in the Interior (I) and the number of border points
(B) varies. Find the areas of each polygon and enter
your results in the table. The first two are done for
you.

|
B
|
I
|
Area
|
3
|
0
|
1/2
|
4
|
0
|
1
|
5
|
0
|
|
6
|
0
|
|
7
|
0
|
|
|
|
|
|
|
|
|
|
|
|
Question: What would be the area of a polygon
that had zero inside points and 15 boundary points?
What did you do to figure out the area for 15
boundary points? Could you have used a rule (in
equation form) to find the answer?
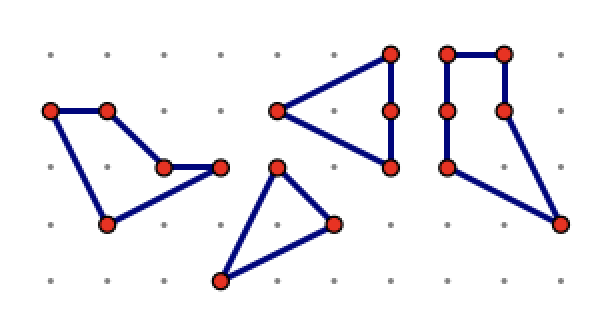
Part 2: Below are some polygons that have 1
interior point. What is the rule (equation)
connecting B and Area for these shapes?
|
B
|
I
|
Area
|
3
|
1
|
|
4
|
1
|
|
5
|
1
|
|
6
|
1
|
|
7
|
1
|
|
|
|
|
|
|
|
|
|
|
|
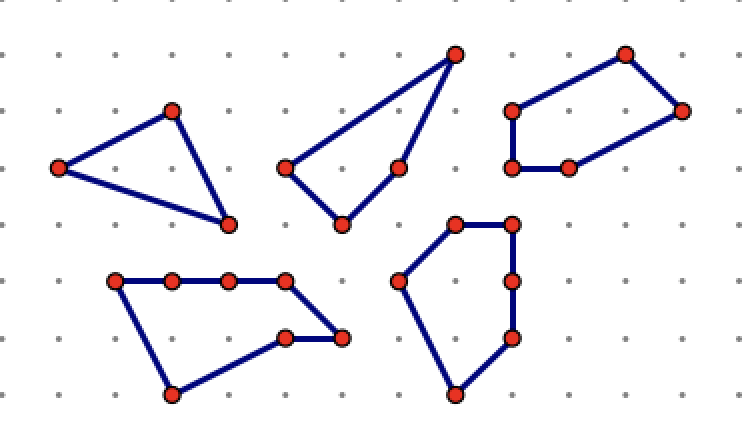
Part 3: Below are some
polygons that have 2 interior points. What is
the rule ( equation) connecting B and Area for
these shapes?
|
B
|
I
|
Area
|
3
|
2
|
|
4
|
2
|
|
5
|
2
|
|
6
|
2
|
|
7
|
2
|
|
|
|
|
|
|
|
|
|
|
|
Part 4: Summarize your findings
from the three tables above. What conclusions
do you draw? Can you write an equation that
lets you find the area (A) from the number of
points on the boundary (B) and points inside
(I)?
*If you don't have Sketchpad you can create the
shapes using Geogebra
or the math
learning center's geoboard.
|
|


