| The Famous Jinx Puzzle |
Teacher's page Revised 9.29.12 |
| This
is
one of my favorite lessons which I usually do with
a prealgebra class.-Ihor The teacher should start out by saying: "Today, I’m going to jinx everyone. Take out your notebook or a piece of paper and do the following steps." 1. Choose a number from 1 to 10 and write it down. 2. Add 11 3. Multiply by 6 4. Subtract 3 5. Divide by 3 6. Add 5 7. Divide by 2 8. Subtract the original number you started with 9. Your Answer is: ________ Teacher asks a
student who is looking up: What did you get?
(13) Teacher: Do you think it matters what number you started with? (Students will not be sure.) Teacher: OK, let's try a few more numbers to see if this pattern continues.The teacher then challenges them to come up with a number that will “break” the jinx. Students try larger numbers, fractions, negative numbers, etc. but come away frustrated declaring that “it must always work” mostly because the task becomes so tedious even with a calculator. At this time the teacher introduces the Jinx calculator. Actually, it’s just a spreadsheet file in disguise that does the calculations for them so they can try more ambitious numbers. After lots of trial and error with no success, the teacher tells the students to try 3000000000000000. (That’s 3 followed by 15 zeros.) Result as expected is still 13. Now click in B1 and add a 16th zero. Surprise! You should see 0. Now does that mean the trick no longer works? Or is it just that our Jinx calculator has some flaws? (It’s the latter.) Spreadsheets “fall apart” when we use numbers out of their range. To prove that the trick really does work all the time, the teachers suggest the use of something that can represent any number chosen including ones you can’t completely write out like pi. The teacher then uses a marbles and bags model and demonstrates why it works using a digital white board. |
A nice way to do this is to use a Powerpoint presentation to highlight each step. Students should say 13. If not, move on to the next student. Ask enough students so the group sees that most students are getting 13. The “correct” answer of course is no, since we can prove it using Algebra. But since this is a prealgebra class the students are usually not sure. What about Pi? An Excel version is available at: http://dmcpress.org/cmdb75/jinxpuzzle/jinx.xls Can that number be used with the Jinx calculator? No, only an approximation like 3.14 is possible.) |
Let's try a different way to answer the question. Start with the puzzle again.
Step 1: Pick a number.
Instead of picking a specific number, let’s choose to use
something that could
represent any number. Let’s use a bag.
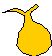
The bag can contain
any number you pick.
Step 2: Add 11


To show 11 we will use 11 small circles or “marbles”. Now
we have a bag and 11 “marbles.”
Step 3: Multiply
by 6
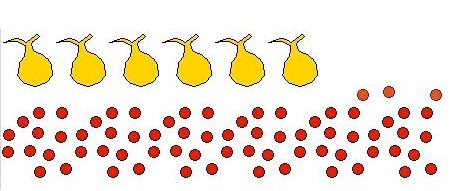
We have 6 bags and 66 marbles.
Step 4: Subtract 3
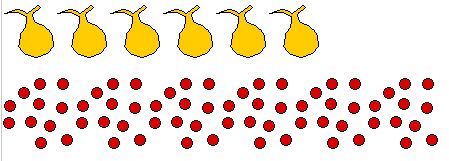
Now we have 6 bags and 63 marbles.
Step 5. Divide by
3
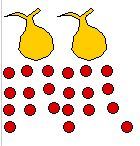
What's left? 2 bags and 21 marbles.
Step 6. Add 5
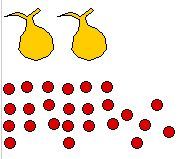
There are 2 bags and 26 marbles.
Step 7. Divide by
2


and we have 1 bag and 13 marbles.
Step 8: Subtract
the number you picked in step 1.

But that’s the bag. You subtract the bag! So you are left
with only 13 marbles or just plain 13.
Can you explain why
this puzzle always gives you 13?
Students should walk away from this activity with an appreciation for the power of variables.