Darts is a challenge that requires players to pop a balloon that appears on a number line between 0 and 1 by throwing fractional darts. This is an excellent game to do once the students have completed a unit/chapter on fractions.
Setting the Stage
Play a fraction game with the students. "I'm thinking of a fraction between 0 and 1.Can you guess it? It must be stated in fractional form with a whole numbers for the numerator and denominator." (Choose 3/4 as your fraction to guess.) A student may guess 1/2. You would say that his or her number is too small. Another student may say 7/8 to which you respond with that's too big. At this point the students may be stuck because they need to find a fraction that is between 1/2 and 7/8. Some students may realize that 3/4 is in between and would guess correctly. An alternative approach is to start with Deducing the "mystery" fraction with your students which does the same activity using an app.
Doing the Activity
At this point have the students go to the menu page and choose the activity Free Play-Darts and explain how Darts works. Have the student's "free play" as you circulate around the room helping students. Students can also help each other in that they are sitting in groups (which is recommended). Also 2 players taking turns is an interesting strategy to follow.
After the students are comfortable with the Free Play version of Darts, have them choose Lesson 1 on the menu page. (It's a good idea for the students to bookmark the menu page.) Then they can continue on to Lesson 2, etc.
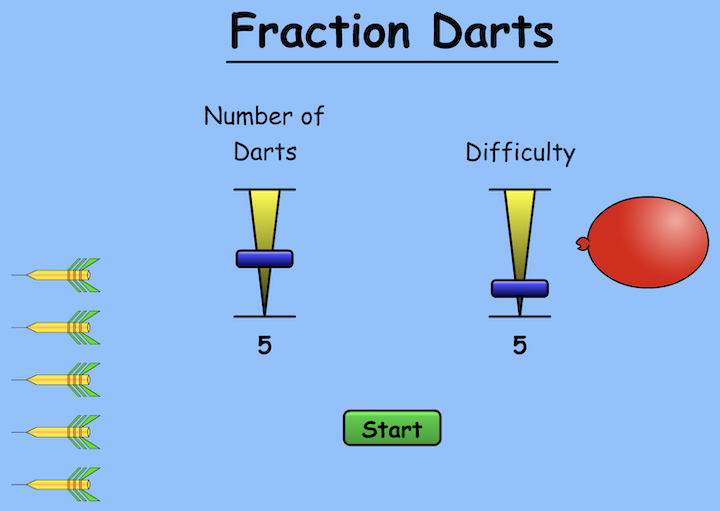 Figure 1
|
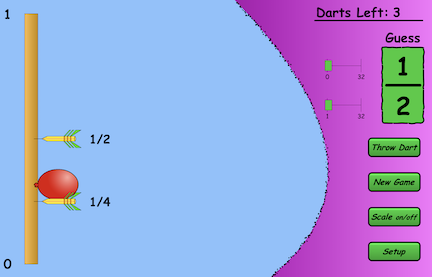 Figure 2 |
Debrief
Ask the students what strategies they discovered. An immediate difficulty that students encounter is how to find a fraction between 2 fractions as in figure 2 above. Finding a number between 1/2 and 1/4 is challenging for students who have a fragile understanding of fractions. One strategy would be to look at 1/2 in an equivalent form, 2/4. Now the two numbers have a common denominator, but you need a number between 1/4 and 2/4. With fractional notation this is a difficult problem to "intuit" since we need to find since numerators are only 1 apart. Realizing that if we now rename 2/4 as 4/8 and 1/4 as 2/8 then the number in between is 11/16. However, there is nothing wrong with an answer like 5.5 / 8. It's just that we are unaccostomed to mixing fractions with decimals. In fact, this problem is much easier if you convert to decimals. What's a number between .25 and .5? But I'm getting ahead of myself. We will deal with decimals playing Decimal Darts. For students who have figured out Fraction Darts and gone through all the links on the student page they can move on with Decimal Darts.
An Interesting Extension
An interesting (though not necessarily pedagogically sound) way to find a number between 3/4 and 5/8 is to add the two numerators (3+5=8) and the two denominators (4+8=12) and form the fraction 8/12 (or 2/3) which just happens to fall between the two original fractions. 2/3’s middle stature can be easily confirmed by looking at the three fractions with the common denominator 24. (18/24; 16/24; 15/24.). Was that just a coincidence or does that always work? It turns out that it always works. Here’s a proof.

References
Scenes from a Dynamic Math Classroom - My Fractions Darts Story
Why are Fractions so Difficult?