Activity: Billiard Paths
Teacher Page
Student Page Challenge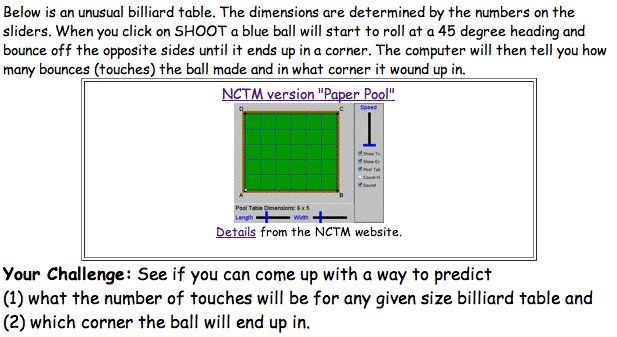

 See notes below.
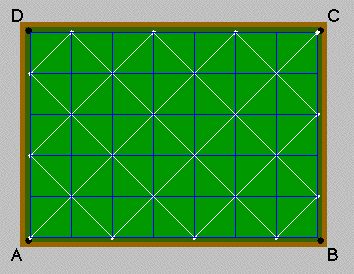
Alert: Answers to questions may appear in parenthesis.
Let's look at a sample student data table. It appears that for the first 5 examples the rule "add length and width and you get the number of touches" seems to work. So why the surprise in example 6? (Hmm..)

W
L
Touches
5
7
 12
8
3
 11
5
4
 9
10
13
 23
 5
 9
 14
 6
 9
 5 (surprise!)

Why did it come up 5 and not 15? Let's look at the path for the 6 by 9 table.

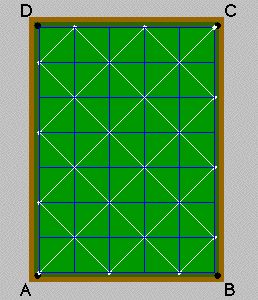
Here are two other paths that also have 5 "touches":

4 by 6 table

2 by 3 table

(Answer coming up.) Note that for the smallest of the three tables the "adding the length and width rule" once again works. The tables have the same path because they are geomtetrically similar which means that their sides are in proportion to each other. Another way of thinking about this is that the ratios of the dimensions are all equal. So if the dimensions are relatively prime, the path will traverse every square and the number of touches will be the sum. Otherwise, find the the smallest rectangle that will have the same path. The sum of its dimensions will give you the number of touches. So the additive rule does work - directly if the length and width are relatively prime - and if they are not then "reduce" the numbers to the smallest possible equivilent table and then add!

Part B - Finding which corner the ball ends up in also has to do with "reduced form" rectangles. Similar paths will always end up in the same corner. So the investigation should be done with paths of relatively prime dimensions.

W
L
Touches
Corner?
5
7
 12
 Top Right (UR)
8
3
 11
 Top Left (TL)
5
4
 9
 Bottom Right (BR)
10
13
 23
 Top Left (TL)
 5
 9
 14
 Top Right (UR)
 6
 9
 5 
 Top Left (TL)*
 7
 10
17
 Bottom Right (BR)

Note that the two odd, relatively prime dimensions both end up in the upper right or opposite corner. If the width is even and the length is odd and they are relatively prime, the width "dominates" and the ball ends up in the Top Left corner. If the opposite is true, then the length dominates and the ball ends up in the Bottom Right corner. Does this always work? (Ahuh.)

If the dimensions are even, which corner will welcome the ball? (It could wind up in any of the three corners. Two even numbers are NOT relatively prime.)

Why can't the ball return to the Bottom Left corner?

Does switching length and width numbers change the final destination? For example, does the ball end up in the same corner for a 7 by 5 table as a 5 by 7 table? (Looks like they do. In both cases the ball starts in pocket A and ends up in pocket C.)

    

*Use the "reduced" 2 by 3 table.

Other Resources

See NCTM's Illumination activity Paper Pool at

http://illuminations.nctm.org/LessonDetail.aspx?ID=L419

Student's Page