 |
 |
 |
 |
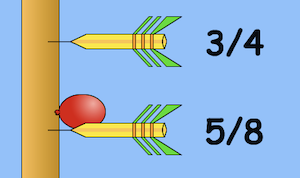
A Conversation Amidst a Darts Challenge
Alice: “So I
need to throw something bigger than 5/8 but smaller than
3/4. Hmm … let me try making the denominator [in
5/8] smaller. Say 5/7?”
John: “Let’s see, 5/7 is smaller than 3/4 but not small enough to hit the balloon.”
Alice: “Whoops. I’ll try 5/9.”
John: “That made it too small, even smaller than 5/8.”
Alice: “We now need something smaller than 5/7 and bigger than 5/8.”
Alice: “Smaller than 5/7? Then it must also be smaller than 10/14. Right? So 10/15 should be smaller, right?”
John: “Let’s try it.” (The balloon pops.) “Bingo!”
Alice: “This is cool!”
Alice discovered a strategy that she wasn’t aware of. Decreasing the denominator by one increased the value of the fraction. Surprise! Alice and John continued playing several more rounds. So what skills did they need to know to eventually pop the balloon?
You can make a fraction smaller if you leave the numerator alone and increase the denominator. (For example, 4/6 is smaller than 4/5.)
You can make a fraction larger if you leave the numerator alone and decrease the denominator. (Revisiting the previous example, 4/5 is bigger than 4/6.)
At first glance, this appears counter-intuitive. But it works because in 4/6, you are dividing your unit into more pieces than 4/5, so each piece of 4/6 will be smaller than 4/5.
I expected the teachers to come up with 11/16, but they surprised me by choosing a trial-and-error way to do it.
John: “Let’s see, 5/7 is smaller than 3/4 but not small enough to hit the balloon.”
Alice: “Whoops. I’ll try 5/9.”
John: “That made it too small, even smaller than 5/8.”
Alice: “We now need something smaller than 5/7 and bigger than 5/8.”
Alice: “Smaller than 5/7? Then it must also be smaller than 10/14. Right? So 10/15 should be smaller, right?”
John: “Let’s try it.” (The balloon pops.) “Bingo!”
Alice: “This is cool!”
Alice discovered a strategy that she wasn’t aware of. Decreasing the denominator by one increased the value of the fraction. Surprise! Alice and John continued playing several more rounds. So what skills did they need to know to eventually pop the balloon?
You can make a fraction smaller if you leave the numerator alone and increase the denominator. (For example, 4/6 is smaller than 4/5.)
You can make a fraction larger if you leave the numerator alone and decrease the denominator. (Revisiting the previous example, 4/5 is bigger than 4/6.)
At first glance, this appears counter-intuitive. But it works because in 4/6, you are dividing your unit into more pieces than 4/5, so each piece of 4/6 will be smaller than 4/5.
I expected the teachers to come up with 11/16, but they surprised me by choosing a trial-and-error way to do it.