Student page (with answers)

Posing the problem
Using a projection device show the student page (without the answers). Ask the question: if you know the measures of angles A and B, could you predict what angle BCD is without measuring?

Hand out the student page and have them measure BCD for all three triangles. Have the students make a chart like this:
 

Have the students use their protractors

They should discover that <BCD = <CAB + <ABC. Use the Sketchpad model (exterior.gsp) to confirm this conjecture. If it appears true, why should that be?

The Secret Behind the Exterior Angle Challenge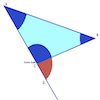

Print out a copy of this image.

Cut out the angles CAB and CBA from image and place them over <DCB. Make sure the vertices A, B and C touches and the angles are adjacent to each other. (See below)

Notice that the angles A and B “fit” the space that the red angle BCD makes. This means that

<A + <B = <BCD

But is it really true? Let’s apply some logic.

We know from a previous lesson that the three blue angles of triangle ABC together add up to a 180 degrees.

What can we say about the blue angle C (ACB) and Angle BCD (the red angle)? Since AC and CD are part of a ray, they form a straight line. That means that angle ACB and angle BCD must also add up to 180 degrees.

Summarizing these results, we see that

<A (blue) + <B (blue) + <C (blue) = 180
<C (red) + <C (blue) = 180

Therefore it must be true that the sum of angle A and Angle B is the same as red Angle C (BCD).

*Build your own Exterior Angle Model using Sketchpad

If the file exterior.gsp is not available, you can construct a model of a triangle with an exterior angle. Here’s how:

1. Open a new sketch in Geometer’s Sketchpad.
2. Use the line segment tool to draw two segments attached at a point and label the end points.

3. Make the third side a ray. Choose the ray tool. (Hold down the line segment tool and slide over and choose the ray tool.



4. Drag the point on the ray so that it lands on point C.


5. Place a point D on the ray AC past point C.




6. Measure Angles A, B, and BCD

Learn More:

We have learned that the exterior angle is between any side of a shape and the line extended from an adjacent side. What if we extended all three sides of a triangle? What would the sum of the 3 exterior angles be? To find out draw this triangle using Sketchpad or Geogebra. Note that the sides are rays. Place a point D on each ray. Measure the angles. (Your angle measurements will differ from the ones below.

What do you notice about the sum of the angle measurements? (They add up to 360º.)
Change the orientation of the triangle. What happened to the angle measures? (They are different, but they still add up to 360.)

Now create a 4 sided polygon. Add the exterior angles. Notice they add up to 360º as well. This will work for any sided polygon.



Here is another way to think about it. In the hexagon below, each line changes direction until we eventually get to the initial position and orientation. In other words, you have turned around one complete turn or 360º. It doesn't matter if it's a triangle, quadrilateral, pentagon or hexagon, the total of the turns equal 360º.


Polygons: Exterior Angles - Revamped

See this website's exploration of exterior angles demonstration done with Geogebra.